怎样用Matlab预测人口
人口预测的模型,主要有阻滞增长模型(logistic),灰色模型GM(1,1),BP网络模型来做。
对于少量的数据,一般用灰色模型GM(1,1)来预测比较多。例如:已知2004-2007的数据48.7, 57.17,68.76,92.15,预测2008、2009、2010的数据。
在命令窗口下运行程序
GM11
得到如下结果

代码如下:
clear all,clc,clear all,clf
X0=input('请输入序列矩阵X: ');%输入数据请用如例所示形式:[48.7 57.17 68.76 92.15],该向量为原始向量X0
n=length(X0);
for i=2:n%开始进行建模可行性分析
Q(i)=X0(i-1)/X0(i);
end
Q(1)=[];
ma=max(Q);
mi=min(Q);
if ma>exp(2/(n+1))
disp(['序列无法进行灰色预测']);
return
elseif mi
return
else
disp(['序列可以进行灰色预测']);
end
%检验结束
X1=cumsum(X0);%累加生成算子向量X1
Z1=ones(n-1,2);
for i=1:(n-1)
Z1(i,1)=-(X1(i)+X1(i+1))/2;
Z1(i,2)=1;%均值生成算子Z1
end
Z1T=Z1';%均值生成算子矩阵Z1的转置Z1T
for j=1:n-1
Y(j)=X0(j+1);
end
YT=Y';
A=inv(Z1T*Z1)*Z1T*YT;%最小二乘估计计算参数a、u
a=A(1); %Z1参数a
u=A(2); %系统给定参数u
disp(['参数a:',num2str(a),' 参数u:',num2str(u)]);
t=u/a;
t_test=input('请输入需要预测个数:');
i=1:t_test+n;
X1S(i+1)=(X0(1)-t).*exp(-a.*i)+t;%计算时间响应序列,得出估计累加向量X1S
X1S(1)=X0(1);
X0S(1)=X0(1);
for j=n+t_test:-1:2
X0S(j)=X1S(j)-X1S(j-1);%计算X1S的逆累加向量X0S
end
for i=1:n
Q(i)=X0S(i)-X0(i);%求残差
E(i)=abs(Q(i))/X0(i);%求相对误差
end
AVG=sum(E)/(n-1);%求平均相对误差
av=input('请输入允许的平均相对误差,如0.1,或0.05:');%输入如0.1,或0.05等形式,不要用5%这类形式
if AVG>=av;%如果平均相对误差大于av%,则进入残差GM模型!!!!!!!
cn=length(Q);
Q1=cumsum(Q);%累加生成算子向量Q1
CZ1=ones(cn-1,2);
for i=1:(n-1)
CZ1(i,1)=-(Q1(i)+Q1(i+1))/2;
CZ1(i,2)=1;%均值生成算子CZ1
end
CZ1T=CZ1';%均值生成算子矩阵CZ1的转置CZ1T
for j=1:cn-1
CY(j)=Q(j+1);
end
CYT=Y';
CA=inv(CZ1T*CZ1)*CZ1T*CYT;%最小二乘估计计算参数ca、cu
ca=CA(1);%CZ1参数a
cu=CA(2);%系统给定参数cu
ct=cu/ca;
i=1:t_test+cn;
Q1S(i+1)=(Q(1)-ct).*exp(-ca.*i)+ct;%计算时间响应序列,得出估计累加向量Q1S
X1S=X1S+Q1S;%将残差拟合值加入,提高精度
for j=n+t_test:-1:2
X0S(j)=X1S(j)-X1S(j-1);%计算X1S的逆累加向量X0S
end
for i=1:cn
Q(i)=X0S(i)-X0(i);%求残差
E(i)=abs(Q(i))/X0(i);%求相对误差
end
AVG=sum(E)/(n-1);%求平均相对误差
end
x=1:n;
xs=2:n+t_test;
yn=X0S(2:n+t_test);
plot(x,X0,'^r',xs,yn,'*-b');%作图
disp(['百分平均相对误差为:',num2str(AVG*100),'%']);
disp(['拟合值为: ',num2str(X0S(1:n+t_test))]);
disp(['预测值为: ',num2str(X0S(n+1:n+t_test))]);
可以用matlab拟合一下logistic人口预测模型吗?,关键是程序和求出的参数。
Logistic人口预测模型是在Malthus模型基础上改进的,该模型考虑有限资源下容纳的最大人口数量Nm。该模型函数表达式为
N(t)=Nm/[1+(Nm/N0-1)*exp(-r*(t-t0))]
式中:N0=6505,t0=1998
现根据题主提供的数据,利用matlab软件对该方程的系数,用回归分析的方法求出其Nm和r值,实现方法如下:
1、输入数据,即
t=1998:2018;
x=[。。。。。。];
2、定义函数,fun=@(a,t)a(1)./(1+(a(1)/6502-1).*exp(a(2)*(t-1998)));
3、使用lsqcurvefit函数,求得系数Nm{fun函数中的a(1)},r{fun函数中的a(2)},即
a=lsqcurvefit(fun,a0,t,x) 其中:a0为初值
4、使用拟合后fun函数,得到拟合后的N(t)值
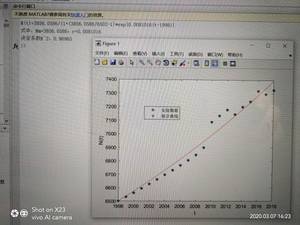
5、使用plot函数绘出拟合前与拟合后的对比图形
6、完善代码后运行可得如下结果。