一个小狗拴在一个等边三角形的墙角,墙边长3绳子长4米,求出小狗能看护的最大面算式
1个r=4m的5/6圆的面积
加上
2个r=(4-3)=1m的1/3圆的面积
S=40/3π+2*(1/3π)
=14π

扩展资料
与圆相关的公式:
1、半圆的面积:S半圆=(πr^2)/2。(r为半径)。
2、圆环面积:S大圆-S小圆=π(R^2-r^2)(R为大圆半径,r为小圆半径)。
3、圆的周长:C=2πr或c=πd。(d为直径,r为半径)。
4、半圆的周长:d+(πd)/2或者d+πr。(d为直径,r为半径)。
5、扇形弧长L=圆心角(弧度制)×R= nπR/180(θ为圆心角)(R为扇形半径)
6、扇形面积S=nπ R²/360=LR/2(L为扇形的弧长)
7、圆锥底面半径 r=nR/360(r为底面半径)(n为圆心角)
于无穷多个小扇形面积的和,所以在最后一个式子中,各段小弧相加就是圆的周长2πR,所以有S=πr²。
5.如图。一只小狗拴在等边三角形的墙角,墙边长3米。绳长4米,求这只小狗最多能看护的面积。
根据题意,小狗能踩到的面积如下草图阴影所示
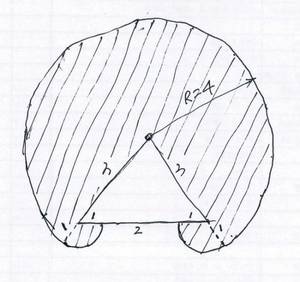
面积=3.14*4^2*(360-60)/360+2*3.14*1^2*120/360=43.96平方米(式中360、60、120为度数,360是圆一圈的度数,等边三角形内角是60度)
一只狗被拴在底座为边长3米的等边三角形建筑物的墙角上,绳长4米,求狗所能到的地方的总面积。
拴狗的绳子长4米,也就是等于圆的半径为4米,我们可以先算一个圆的面积:4²×3.14=50.24(m²) 等边三角形的每个角为60°,一个圆为360°,因此狗活动的范围只有圆的360分之300,也就是6分之5。拴狗的绳子是4米,比三角形的边长了1米,因此他活动的范围还有左右两个3分之1的圆,也就是3分之2的圆,所以可以综合算式:50.24×6分之5+1²×3.14×3分之2=43.96(m²) 虽然晚了,但希望能采纳一下,可以帮助到更多的人!一只狗被拴在底座为边长3米的等边三角形建筑物的墙角上绳长是4米狗所能到达的
3.14*4^2*300/360+2*3.14*(4-3)^2*120/360 =3.14*(80/6+2/3) =3.14*14=43.96 是一个圆心角为360-60=300度,半径4米的扇形;和两个半径是4-3=1米,圆心分别是另外两个墙角,圆心角是120度的扇形的面积的总和。 [百度参考]一只狗栓在一个边长为3米得等边三角形建筑物的墙角,如图,绳长4米,求狗所能到得地
应该是直径为4米的圆的300度扇形面积,再加上2个直径为1m的圆的120度的扇形的面积。
狗从一个墙角到另一个墙角时,绳会被墙角挡住。
