树和二叉树之间有怎么样的区别与联系
1、两者性质不同
树是一种数据结构;二叉树是每zhi个结点最多有两个子树的一种树结构。
2、结点数目不同
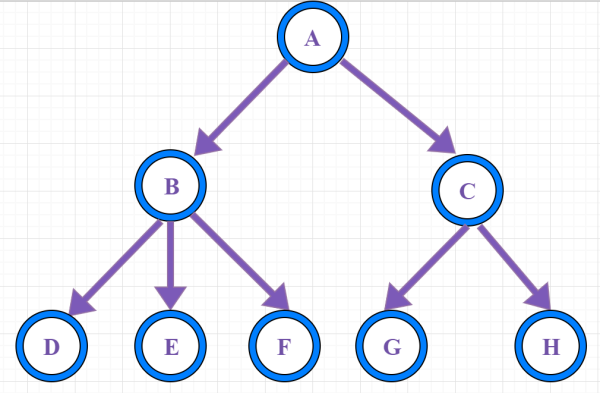
树的每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点。
二叉树:每个结点最多有两个子树。
树和二叉树的联系:树都可用二叉链表作为存储结构,对比各自的结点结构可以看出,以二叉链表作为媒介可以导出树和二叉树之间的一个对应关系。从物理结构来看,树和二叉树的二叉链表是相同的,只是对指针的逻辑解释不同而已。
从树的二叉链表表示的定义可知,任何一棵和树对应的二叉树,其右子树一定为空。
扩展资料
二叉树的类型
(1)完全二叉树——若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
(3)平衡二叉树——平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
辨析
二叉树是树的一种特殊情形,是一种更简单而且应用更加广泛的树。
R树的定义
一棵R树满足如下的性质:
1.除根结点之外,所有非根结点包含有m至M个记录索引(条目)。根结点的记录个数可以少于m。通常,m=M/2。
2.对于所有叶子中存储的记录(条目),I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形(注意:此处所说的“矩形”是可以扩展到高维空间的)。
3.对于所有非叶子结点上的记录(条目),i是最小的可以在空间上完全覆盖这些条目所代表的点的矩形(同性质2)。
4.所有叶子结点都位于同一层,因此R树为平衡树。
