请列出1~100兀表,要有答案。
π= 3.14 2 π= 6.28 3 π= 9.42 4 π= 12.56 5 π= 15.7 6 π= 18.84 7 π= 21.98 8 π= 25.12 9 π= 28.26 10 π= 31.4 11 π= 34.54 12 π= 37.68 13 π= 40.82 14 π= 43.96 15 π= 47.1 16 π= 50.24 17 π= 53.38 18 π= 56.52 19 π= 59.66 20 π= 62.8 21 π= 65.94 22 π= 69.08 23 π= 72.22 24 π= 75.36 25 π= 78.5 26 π= 81.64 27 π= 81π到100π数值表
1π到100π数值表如下:
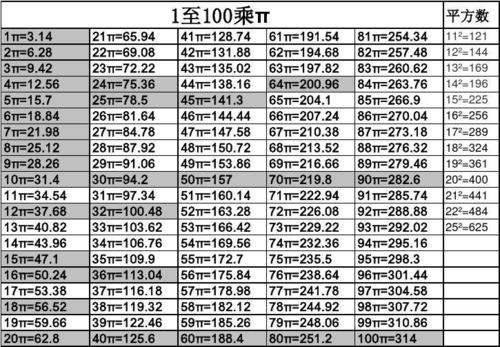
圆周率用希腊字母π(读作pài)表示,是一个常数(约等于3.141592654),是代表圆周长和直径的比值。它是一个无理数,即无限不循环小数。在日常生活中,通常都用3.14代表圆周率去进行近似计算。
扩展资料
历史上最马拉松式的人手π值计算,其一是德国的鲁道夫·范·科伊伦(Ludolph van Ceulen),他几乎耗尽了一生的时间,于1609年得到了圆周率的35位精度值,以至于圆周率在德国被称为Ludolphine number。
其二是英国的威廉·山克斯(William Shanks),他耗费了15年的光阴,在1874年算出了圆周率的小数点后707位,并将其刻在了墓碑上作为一生的荣誉。可惜,后人发现,他从第528位开始就算错了。
π1到100的公式是什么?
1π到100π数值表如下:
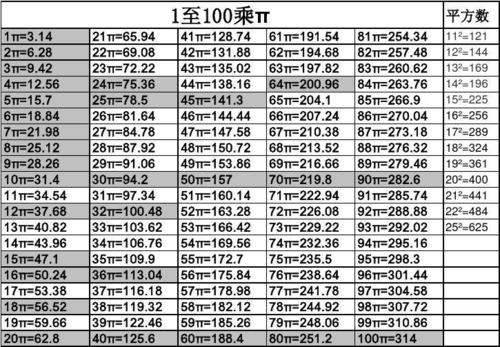
圆周率用希腊字母π(读作pài)表示,是一个常数(约等于3.141592654),是代表圆周长和直径的比值。它是一个无理数,即无限不循环小数。在日常生活中,通常都用3.14代表圆周率去进行近似计算。
相关内容解释:
圆周率(Pai)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比。是精确计算圆周长、圆面积、球体积等几何形状的关键值。 在分析学里,π可以严格地定义为满足sin x = 0的最小正实数x。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。而用十位小数3.141592654便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
圆周率1到100位?
圆周率1到100位分别是:3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679。

扩展资料:
圆周率的计算方法是圆周长除以直径。“圆周率”是圆的周长与直径的比值。,
圆周率,用希腊字母π表示(发音为pai),是一个常数(约为3.141592653),它代表了圆的周长与直径的比率。它是一个无理数,也就是无限的不循环小数。
在日常生活中,常用3.14来表示圆周率进行近似计算。十进位3.141592653对于一般计算就足够了。即使工程师或物理学家要进行更复杂的计算,他们最多也需要到小数点后几百位。
在很长一段时间里,中国在圆周率的计算上领先世界,这要归功于魏晋时期数学家刘辉创造的“切圆”的新方法。
所谓“圆切割技术”,就是利用圆内正多边形的周长无限近似圆的周长,从而得到圆周率。这种方法是刘辉在批判和总结了数学史上各种旧的计算方法之后所创立的一种新方法。
圆周率1到100位分别是什么?
圆周率1到100位分别是3. 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679。
圆周率前100位口诀
3 . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6
山巅一寺一壶酒,尔乐苦煞吾,把酒吃,酒杀尔,杀不死,乐尔乐。
4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9 7 1 6 9 3 9 9 3 7
死珊珊,霸占二妻。 救吾灵儿吧! 不只要救妻, 一路救三舅, 救三妻。
5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7
吾一拎我爸,二拎舅(其实就是撕吾舅耳)三拎妻。
8 1 6 4 0 6 2 8 6 2 0 8 9 9 8 6
不要溜!司令溜,儿不溜!儿拎爸,久久不溜!
2 8 0 3 4 8 2 5 3 4 2 1 1 7 0 6 7 9
饿不拎,闪死爸,而吾真是饿矣!要吃人肉?吃酒!

扩展资料:
圆周率是用圆的周长除以它的直径计算出来的。“圆周率”即圆的周长与其直径之间的比率。
圆周率用希腊字母π(读作pài)表示,是一个常数(约等于3.141592653),是代表圆周长和直径的比值。它是一个无理数,即无限不循环小数。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。而用十位小数3.141592653便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
我国古代在圆周率的计算方面长期领先于世界水平,这应当归功于魏晋时期数学家刘徽所创立的新方法——“割圆术”。
所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。这个方法,是刘徽在批判总结了数学史上各种旧的计算方法之后,经过深思熟虑才创造出来的一种崭新的方法。