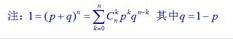贝努利概率在抛硬币中的困惑
首先假设所处环境和所用硬币以及抛掷手法对于我们的分析是公正的,硬币抛一次,正反两面几率都是百分之五十。这是前提。接下来继续讨论 事实上无论你前15次是什么结果,第16次抛出的硬币正反概率都是百分之五十。因为每次抛硬币是独立事件,互相不影响。 再者你是不是承认这点:掷16次为一轮,一直这么做很多近似于无穷轮,这其中肯定有许多轮,前15次都是正面。那么在这些轮中,前15正第16反这种情况和前15正第16还是正,这两种情况,你觉得那种更容易发生,并给出理由,我是觉得两者是一样的。 最简单的第一次正第二次反和前两次都是正的概率没理由不一样吧。既然一样,前两次正第三次反和前三次都是正的概率也是一样吧。那如何用minitab进行分布检验
如何检验你的离散数据分布
我们研究过不同的离散分布以及如何使用它们。在这篇文章中,我将阐述如何确定你的数据是否遵循特定的离散分布。
在检测离散分布之前,我们需要区分两种情况。有时,更重要的是:
检查假定条件(二期分布)
执行拟合优度检验
检查使用二项分布的前题假设
对于二项分布来说,你需要确定你的数据是否满足该分布的假设。如果满足前题假设,您可以使用这个分布来为过程建模。
通过一个例子,我们来了解一下二项分布的假设。二项分布具有以下四个假设:
1.每个试验都有两种结果:这可能是通过或失败,接受或拒绝等。
2.每个试验都是独立的:如果每个可能的结果都不会随着实验次数的不同而改变,那么在实验中,每次实验验证都是独立的。举个例子,你抛掷硬币50次,每抛掷一枚硬币是一个独立的事件,因为抛掷(正面和反面)的结果不会影响下次抛掷硬币正反面的可能性。
3.在实验中,每个事件的概率都是相同的:概率不会随着时间而变化。有时由于涉及的物理特定属性,比如抛掷一枚硬币,你也可以做出这样的假设。其他时候,你可能想要使用P图来验证这个假设。如果P控制图是受控的,那么概率是一个定值。
4.试验的次数是固定的:这种假设反映了你的目标,你想要建立的模型在特定实验次数下发生的频率。
一般来说,如果要确定你的数据是否满足这些假设,通常依赖于对生产过程的紧密理解,数据收集的步骤,以及你收集数据的目的。如果满足了所有这些假设,您可以放心地使用二项分布。
除了二项分布之外,在Minitab统计软件中,还有其他三个分布也会涉及二项分布。与二项分布相比,它们各自都有不同的假设。
简而言之,如果你有二项数据,选择使用哪种分布,取决于总体的情况,比率的稳定性以及你想如何使用这些数据。在验证了这些假设之后,您通常不需要进行拟合优度检验。
执行拟合优度检验
如果你觉得你的数据服从泊松分布或者基于属性数据的其它分布,你应该进行拟合优度检验以确定数据所属的特定分布。这些检验将观测值与理论值进行比较,从而确定二者是否有显著差异。我们将列举一些实例,这样你就能体会到执行这些检验是多么容易。
分布
如果你想确定数据是否遵循泊松分布,你可以使用Minitab软件中专门的分布检验工具。回顾一下PoIsson分布描述的是常数观测值的统计特性(比如缺陷等…) ,例如挡风玻璃划痕的数量。
缺陷数示例
一位保险经纪人希望估测在特定的十字路口每月发生事故的数量,他在工作表中记录的事故数量是这样的:
工作表中每个单元格的值代表的是每个月事故的数量。
In在Minitab中。选择统计>>基本统计量中的Poisson分布的拟合优度检验,在变量中输入Accidents,点击确定
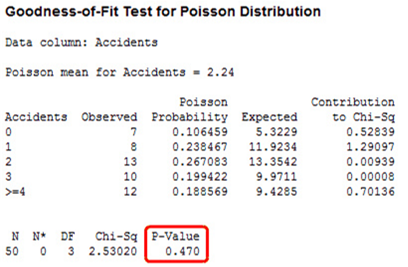
P值为0.470,大于α水平0.05。结果表明,这些数据服从Poisson分布,可以使用这个假设进行分析。这些分析包括单样本和双样本Poisson比率,U控制图,Laney U '控制图。
分类分布
你可以在Minitab中使用”卡方拟合优度检验”对分类数据进行分析,这是类似于Poisson分布的拟合优度检验。只是Minitab软件不知道你的数据所属的分布,您需要亲自指定针对比率的检验。
汽车颜色示例
我们将使用先前博客中汽车颜色的比率的例子来进行演示。在这个例子中,由PPG公司报道的全球比率的数据是真实的,而我们“收集”的观测值只用于演示。
假设想要确定:在我们国家的汽车颜色在全球分销商中的分布情况。要得到这些信息,我们分布在全国的观察者记录了在2012年的随机样本中制造汽车的颜色。我们收集了颜色数据,并输入到下面的全球分布工作表中:
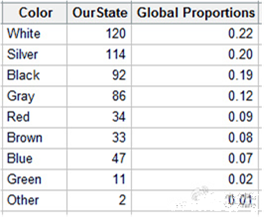
在OurState列中,数据表示的是样本中每个颜色的统计结果,而Global Proportions是PPG公司报告中的数据。
在Minitab中,选择统计>表格>卡方拟合优度检验(单变量),在对话框的实测计数中输入OurState,在类别名称中输入颜色,在检验下选择特定比率,然后输入GlobalProportions,点击确定。
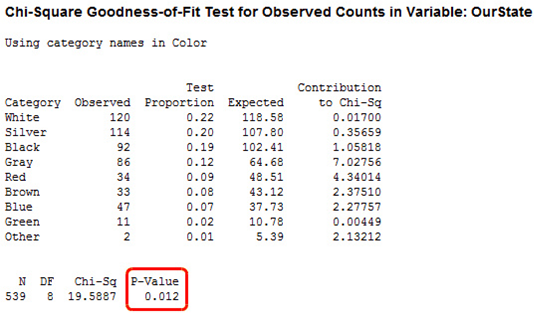
Minitab检查实测计数与全球分布是否存在显著差异。较低的P值表明,数据不服从该分布。在这种情况下,假设检验的P值为0.012,这表明我们国家汽车颜色的分布与全球的分布不一致。你可以比较观测值和表格中预期列的数据之间最大的差异在哪里,或者看看下面的默认图形。

上图显示了哪些颜色在统计上的贡献最为显著。灰色和红色的贡献最多,超过了一半。但是图形没有显示观测值是否高于或低于预期值。下一个图形显示了这些内容。

看看上面图形中“灰色”和“红色”的条形。灰色汽车的观测计数大于预期的计数;相反,红色汽车的观测计数小于预期的计数。
总结
我们讨论了多种离散数据,以及在使用离散分布模型之前如何进行检验。为了确定如何使用你的离散数据,首先你需要确定数据类型或者可能的类型。让我们快速进行总结:
l二项数据:检验二项数据的前题假设
lPoisson数据:使用Poisson分布的拟合优度检验
l其它类型数据:使用卡方拟合优度检验并指定检验比率
假设硬币是公平的,抛出硬币得到正面和反面的概率相同,抛出99次,每次都得到正面
抛硬币为马氏链,既考察一个随机过程,若己知现在t的状态X(t),那么将来的状态X(t+n)取值(或取某些状态)的概率与过去状态X(s)(s抛硬币是0-1分布还是二项分布?
0-1分布是二项分布当n=1时的特殊情形
二项分布是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。举个例子就是,独立重复地抛n次硬币,每次只有两个可能的结果:正面,反面,概率各占1/2。
设A在n重贝努利试验中发生X次,则
并称X服从参数为p的二项分布,记为: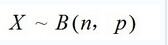
与此同时,