如图,已知边长为3的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的
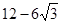 |
| 根据轴对称的性质可得AE=ED,在Rt△EDC中,利用60°角求得ED= 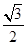 EC,列出方程EC+ED=(1+ EC,列出方程EC+ED=(1+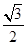 )EC=3,解方程即可求解. )EC=3,解方程即可求解.解:∵AE=ED 在Rt△EDC中,∠C=60°,ED⊥BC, ∴ED= 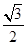 EC, EC,∴CE+ED=(1+ 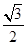 )EC=3, )EC=3,∴CE=12-6 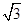 . .故答案为:12-6 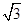 . . |
已知△ABC是等边三角形,E是AC边上一点,F是BC边延长线上一点,且CF=AE,连接BE、EF.
(1)根据等腰三角形三线合一的性质可得∠CBE=1/2∠ABC=30°,AE=CE,所以CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明;
(2)图2,过点E作EG∥BC,交AB于点G,根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,然后根据等边三角形的性质得到AB=AC,∠ACB=60°,再求出△AGE是等边三角形,根据等边三角形的性质得到AG=AE,从而可以求出BG=CE,再根据等角的补角相等求出∠BGE=∠ECF=120°,然后利用“边角边”证明△BGE和△ECF全等,根据全等三角形对应边相等即可得证;
(3)图3,证明思路与方法与图2完全相同.
(1)答:猜想BE与EF的数量关系为:BE=EF;
证明:(1)∵△ABC是等边三角形,E是线段AC的中点,
∴∠CBE=1/2∠ABC=30°,AE=CE,
∵AE=CF,
∴CE=CF,
∴∠F=∠CEF,
∵∠F+∠CEF=∠ACB=60°,
∴∠F=30°,
∴∠CBE=∠F,
∴BE=EF;
(2)答:猜想BE=EF.
证明如下:如图2,过点E作EG∥BC,交AB于点G,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
在△BGE与△ECF中,
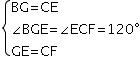
,
∴△BGE≌△ECF(SAS),
∴BE=EF;
(3)BE=EF.
证明如下:如图3,过点E作EG∥BC交AB延长线于点G,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴在△BGE与△ECF中,
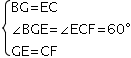
,
∴△BGE≌△ECF(SAS),
∴BE=EF.
等边三角形ABC中,AB=3,点D在直线BC上,点E在直线AC上,且∠BAD=∠CBE,当BD=1时,则AE?
2或4或9/2或9/4 解析 分四种情形分别画出图形,利用全等三角形或相似三角形的性质解决问题即可; 分四种情形:①如图1中,当点D在边BC上,点E在边AC上时.   ∵△ABC是等边三角形,∴AB=BC=AC=3,∠ABD=∠BCE=60°, ∵∠BAD=∠CBE,∴△ABD≌△BCE(ASA),∴BD=EC=1,∴AE=AC﹣EC=2. ②如图2中,当点D在边BC上,点E在AC的延长线上时.作EF∥AB交BC的延长线于F. ∵∠CEF=∠CAB=60°,∠ECF=∠ACB=60°, ∴△ECF是等边三角形,设EC=CF=EF=x, ∵∠ABD=∠BFE=60°,∠BAD=∠FBE,已知三角形ABC是等边三角形,分别在AC,BC上去取点E,F,且AE=CF,BE、AF交于点D,则
已知三角形ABC是等边三角形,分别在AC、BC上取点E,F,且AE=CF,BE、AF交于点D,则∠BDF=多少? 在△BAE和△ACF中, AB = AC ,∠BAE = 60°= ∠ACF ,AE = CF , 所以,△BAE ≌ △ACF , 可得:∠ABE = ∠CAF , ∠BDF = ∠ADE = ∠BEC-∠CAF = ∠BEC-∠ABE = ∠BAE = 60°。(2014?锦州一模)如图,在边长为3的等边三角形ABC中,E,F,P分别为AB,AC,BC边上的点,且满足AE=FC=CP
解答:证明:(1)在△AEF中,∵AE=1,AF=2,∠EAF=60°,由余弦定理可得EF2=12+22-2×1×2×cos60°=3,
∴AE2+EF2=AF2,∴EF⊥AE.即A1E⊥EF.
又平面A1EF⊥平面FEBP,∴A1E⊥平面FEBP.
∴A1E⊥PF.
(2)取A1E的中点M,连接QM,MF.
又∵Q为A1B的中点,∴QM
| ∥ |
. |
| 1 |
| 2 |
∵FC=CP=1,∠C=60°.
∴△CFP是等边三角形.
∴∠CPF=∠B=60°,
∴PF∥BE.PF=
| 1 |
| 3 |
| 1 |
| 2 |
∴QM
| ∥ |
. |
∴四边形PQMF为平行四边形,
∴PQ∥MF.
∵MF?平面A1EF,PQ?平面A1EF.
∴PQ∥平面A1EF.