一个圆柱形茶叶筒的侧面粘着商标纸，圆柱底面半径是5cm，高是20cm。这张商标纸的面积是多少？
一、一个圆柱形茶叶桶的侧面贴着商标纸，圆柱底面半径5厘米，高20厘米，这张商标纸的面积是628平方厘米，这个茶叶桶的体积是785立方厘米。解析如下：1、商标面积：二乘以五乘以三点一四乘以二十等于628平方厘米
2、体积：三点一四乘以五乘以五乘以二十等于785立方厘米。
圆柱是由以矩形的一条边所在直线为旋转轴，其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
一个圆柱形的茶叶筒的侧面贴着商标纸，圆柱底面半径是5厘米，高是20厘米，这张商标纸的面积是多少？
因为是在侧面贴，所以就是求侧面积，商标纸的面积就是2πrh=2×3.14×5×20=628平方厘米。一个圆柱形茶叶筒的侧面贴着商标纸，圆柱底面半径是5厘米，高是二十厘米。这张商标纸的面积是多少
一、一个圆柱形茶叶桶的侧面贴着商标纸，圆柱底面半径5厘米，高20厘米，这张商标纸的面积是628平方厘米，这个茶叶桶的体积是785立方厘米。解析如下：
1、商标面积：2x5x3.14x20=628平方厘米
2、体积：3.14x5x5x20=785立方厘米
3、如图
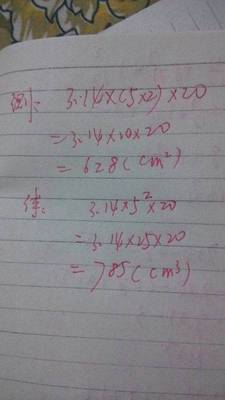
二、拓展资料
关于圆柱
1、圆柱(circular cylinder)是由以矩形的一条边所在直线为旋转轴，其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
2、定义
1、如下图，以矩形的一边所在直线为旋转轴，其余三边旋转360°形成的曲面所围成的几何体叫作圆柱(circular cylinder)，即矩形ADD'G的一条边AG为轴，其余三边旋转一周所得的几何体。其中AG叫做圆柱的轴，AG叫做圆柱的高，无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线
。DA和D'G旋转形成的两个圆叫做圆柱的底面，DD'旋转形成的曲面叫做圆柱的侧面。
2、在同一个平面内有一条定直线和一条动线，当这个平面绕着这条定直线旋转一周时，这条动线所成的面叫做旋转面，这条定直线叫做旋转面的轴，这条动线叫做旋转面的母线。如果母线是和轴平行的一条直线，那么所生成的旋转面叫做圆柱面。如果用垂直于轴的两个平面去截圆柱面，那么两个截面和圆柱面所围成的几何体叫做直圆柱，简称圆柱。
3、与圆锥的关系
等底等高的圆锥积是圆柱体积的三分之一。
体积和高相等的圆锥与圆柱，圆锥的底面积是圆柱的三倍。
体积和底面积相等的圆锥与圆柱，圆锥的高是圆柱的三倍。
等底等高间圆柱与圆锥之间的侧面积之比关系为： S圆柱侧/S圆锥侧=
，其中，r为底面半径，h为高。
（参考资料：百度百科：圆柱）
一个圆柱形茶叶桶的侧面贴着商标纸，圆柱底面半径5厘米，高20厘米，这张商标纸的面积是多少平方厘米？
一个圆柱形茶叶桶的侧面贴着商标纸，圆柱底面半径5厘米，高20厘米，这张商标纸的面积是628平方厘米，这个茶叶桶的体积是785立方厘米。
1.商标面积
2x5x3.14x20=628平方厘米
2.体积
3.14x5x5x20=785立方厘米
如图
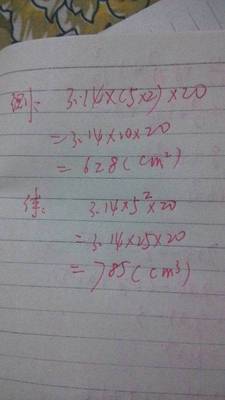
拓展资料
圆柱是由以矩形的一条边所在直线为旋转轴，其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。